Support Vector Machine

Support Vector Machine

• Support Vector Machine은 모델이다.
• hyperparameter는 C와 gamma
• 주로 사용하는 손실함수는 힌지손실 Hinge Loss

Reference : 핸즈 온 머신러닝, 머신러닝 도감, 사이킷런 홈페이지

마진이 아래 식으로 구해지는 이유

• margin = \(\frac{2}{||w||}\)

어딘가의 SVM lecture 노트임!

image

• 샘플들을 서포트벡터라고 보자
• 마진은 \(\frac{2}{||w||}\)
• 점 하나가 랜드마크. 랜드마크를 어떤 기준으로 뽑을 것임.
• 그 기준으로 슬랙 변수를 계산할건데

image.png

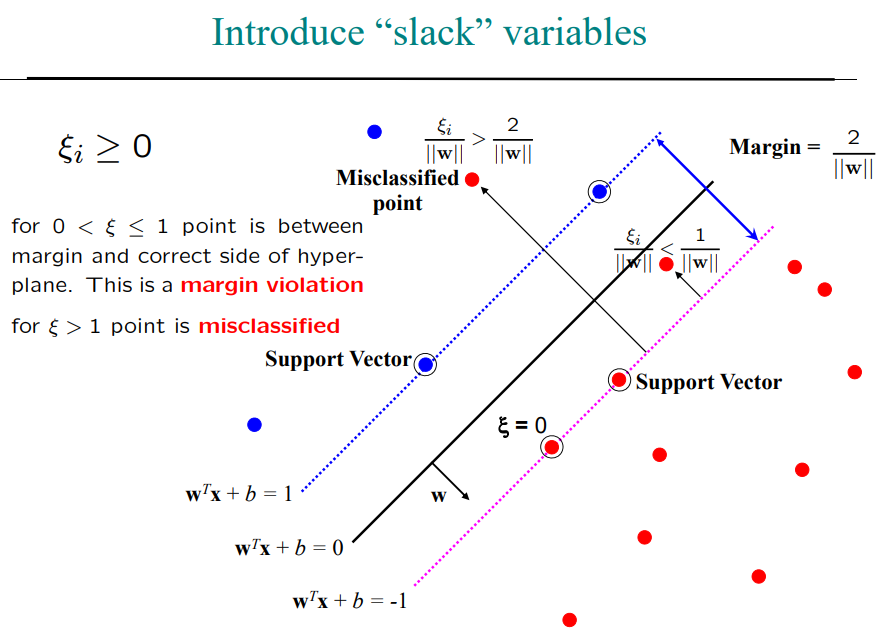
• 위의 경우는 소프트 마진에 한 함
• 마진 경계선으로부터 반대쪽까지 거리를 슬랙 변수로 정의함
• 경계에 걸치면 슬랙변수는 0이 됌.
• 0과 1사이에 있으면 마진 오차 margin violation
• 2보다 크다면 잘못 분류됨 misclassified
• 소프트 마진에서는 1이나 -1이 아니라 \(1- \zeta_1\)을 기준으로 경계선이 나눠져서!
• 소프트 마진에서는 하이퍼파라미터 C를 거의 0으로 만들어서 하드 마진처럼 strick 하게 만들 수 있음

힌지 손실 Hinge Loss

• \(max(0,1-t)\) function
• \(t=1\)에서 미분가능하지 않지만 \(t=1\)에서 서브그레디언트로 경사 하강법 사용

1. 선형 SVM 분류

• 클래스가 선형으로 분류될 때
• 클래스 분류의 경계에 있는 샘플 = 서포트 벡터

1) 하드 마진 분류

• 클래스 분류의 경계에 샘플이 없을 때 = 마진 오류가 하나도 없을때, 하드 마진 분류

  • 선형적으로 구분되어야 함
  • 이상치에 민감함

이 때 생기는 이상치를 마진 오류로 본다.

• 이상치 \(\to\) 클래스 구분했을때 그어지는 선에 걸쳐지는 값들 \(\to\) 마진 오류 margin violation

적절한 균형 잡는 것이 필요

\(minimize_{w,b} ||w||^2_2\)

subject to \(y_i(w^\top x_i - b) \ge 1 \forall_i \in \{1, \dots , n \}\)

• 거의 불가능..한 자료 구조..

2) 소프트 마진 분류

소프트 마진 분류 필요한 이유.

• hyper parameter C가 너무 크면 과대적합 가능성 존재

손실함수는 힌지 손실 Hinge Loss

• 주로 SVM과 함께 쓰임. \(max(0,1-y), max(0,1+y)\) 로 \(y\)의 범위가 [-1,1]에 오도록 함

\(minimize_{w,b,\zeta} ||w||^2_2 + C\sum^n_{i=1} \zeta_i\)

subject to \(y_i(w^\top x_i - b) \ge 1-\zeta_i, \zeta_i \ge 0 \forall_i \in \{ 1 ,\dots, n\}\)

• \(1-\zeta_i\)로 잡음으로써 더 유연하게 이상치 정의 및 경계선 정의

• 위처럼 선에 걸친게 마진 오류 margin violation

2. 비선형 SVM 분류

• 선형적으로 분류할 수 없는 데이터셋에 한해서, 2차, 3차,.. 등

1) 다항식 커널

• 다항식은 잘 작동하기는 한데 설명변수가 너무 많아지면 오히려 모델을 느리게 만들어서 안 좋아..

2) 유사도 특성

• 특정 랜드마크와 얼마나 닮았는지 유사도 함수 similarity function = similarity measure = similarity metric 로 계산¹
  • 특정 랜드마크 -> 데이터 분포가 있을떄 뽑아진 임의의 점?

유사도 함수의 종류

• 유클리디안 거리 Euclidean Distance ; 모든 속성 고려
• 코사인 유사도 Cosine Similarity ; 각으로 고려; -1~1사이
• 마할라라비스 거리 ; 값들 사이의 공분산 이용
• 민코스키 거리 Minkowski Distance ; 가장 큰 값만 고려

3) 가우시안 RBF 커널²

• Gaussian Radical Basis Function = Gaussian Kernel

4) 계산 복잡도

\(O(m\times n)\)

computational complexity theory

3. SVM 회귀

SVM은 선형, 비선형 분류 뿐만 아니라 선형, 비선형 회귀에도 사용

• 마진을 크게하든지(오른쪽) 작게하든지(왼쪽) 영향을 받지 않는다면, 민감하지 않다고 표현

image.png

4. SVM 이론

1) 결정 함수와 예측

선형 SVM을 훈련한다 = 마진 오류를 하나도 발생하지 않거나(하드 마진) 제한적인 마진 오류를 가지면서(소프트 마진) 가능한 한 마진을 크게 하는 \(\mathbb{w}\)와 \(b\)를 찾는 것

단순히 선형 회귀식 계산해서 0인지 1인지를 나눈다.

\(\hat{y} = \begin{cases} 0 & \mathbb{w}^\top \mathbb{x} + b < 0 \text{ 일 때} \\ 1 & \mathbb{w}^\top \mathbb{x} + b \ge 0 \text{ 일 때} \end{cases}\)

2) 목적 함수

결정 함수의 기울기는 가중치 벡터의 노름 \(||w||\)와 같다.

• 마진 크게 = \(||w||\) 최소화

하드 마진 선형 SVM 분류기의 목적 함수

\(minimize_{w,b} \frac{1}{2} \mathbb{w^\top w}\)

\(\star\) 왜 \(\frac{1}{2} \mathbb{w^\top w}\)? \(||w||\)는 \(w=0\)에서 미분도 되지 않음

소프트 마진 선형 SVM 분류기의 목적 함수

• 슬랙 변수 slack variable \(\zeta^{(i)} \ge 0\) 도입
  • i번째 샘플이 얼마나 마진을 위반할지 정함
  • \(x > b\)
  • \(x = b + slack\)

-> 슬랙변수는 경계를 나눌때 생기는 최소한의 오차로 생각하자

마진 오류 최소화 방법

1. 슬랙 변수 값을 작게 만들기
2. 마진 크게 하기 위해 \(\frac{1}{2} \mathbb{w^\top w}\) 최소화

\(minimize_{w,b,\zeta} \frac{1}{2} \mathbb{w^\top w} + C \sum^m_{i=1}\zeta^{(i)}\)

\(\star\) hyper parameter \(C\) \(\to\) 두 목표object 사이의 트레이드 오프 정의

3) 콰드라틱 프로그래밍

콰드라틱 프로그래밍 Quadratic Programming, QP = 하드 마진과 소프트 마진 문제는 모두 선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제

4) 쌍대 문제

5) 커널 SVM

원래 선형 분리할 수 없는 비선형 데이터를 커널을 통해서 선형화 시킴!

\(\star\) 가우시안 커널이 복잡한 결정 경게를 학습한다고 데이터에 무조건 비선형 커널 기법을 적용하지 말고(분석에 의미가 없을 수 있음), 선형 커널을 이용한 분석으로 확린 후 커널 함수를 적용한 분석을 하는 것이 좋음

image

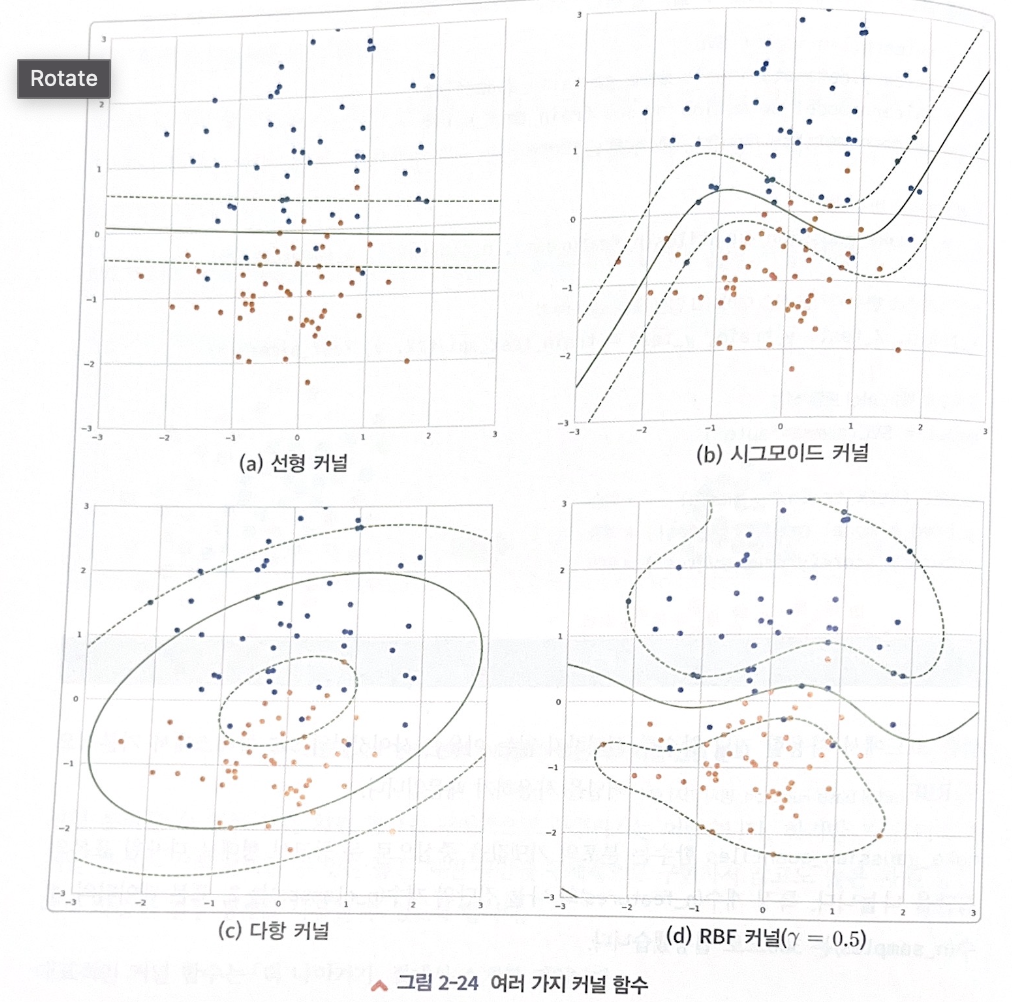
커널의 종류

• 선형 커널 linear kernel 예시, 선형, 비선형 포함
  • \(<x,x'>\)
• 시그모이드 커널 sigmoid kernel
  • \(\tanh(\gamma<x,x'>+r)\)
  • where \(r\) is specified by coef0.
• 다항 커널 polynomial kernel
  • \((\gamma<x,x'> + r)^d\)
  • where \(d\) is specified by parameter degree, \(r\) by coef0.
• RBF 커널 = 가우시안 커널 rbf kernel
  • \(exp(-\gamma||x - x'||^2)\)
  • where \(r\) is specified by parameter gamma, must be grater than 0
    • 복잡한 결정 경계 다룰때 좋을 듯

image.png

쓰는 법

linear_svc = svm.SVC(kernel='linear')
linear_svc.kernel

선형 커널

linear_svc = svm.SVC(kernel='sigmoid')
linear_svc.kernel

시그모이드 커널

linear_svc = svm.SVC(kernel='poly')
linear_svc.kernel

다항 커널

rbf_svc = svm.SVC(kernel='rbf')
rbf_svc.kernel

rbf 커널

6) 온라인 SVM

SVM과 로지스틱 회귀의 차이

둘 다 지도학습이다!

• SVM은 경계면으로 데이터 classification, 로지스틱은 시그모이드 함수로0~1 사이 확률값 추정해서 분류
• 대용량 데이터에서는 SVM이 적당, 로지스틱 회귀는 느리다
• multi-class를 위해 로지스틱 회귀 이용, SVM은 이진 분류만 가능
• 슬랙변수 쓰는 SVM은 이상치에 덜 민감함, 하지만 로지스틱은 이런 역할 하는 변수 없어서 민감

예제

SVM

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 데이터 분류의 중심 위치 정의
centers = [(-1, -0.125), (0.5, 0.5)]

# 특징과 종속 변수 생성
X, y = make_blobs(n_samples=50, n_features=2, centers=centers, cluster_std=0.3)

# 특징과 종속 변수 각각을 학습 데이터와 검증 데이터로 나누기
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 선형 서포트 벡터 머신 모델 생성
model = LinearSVC()

model.fit(X_train, y_train)    # 학습
y_pred = model.predict(X_test) # 예측
accuracy_score(y_pred, y_test) # 평가

커널 기법 이용

from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 특징과 종속 변수 생성
X, y = make_gaussian_quantiles(n_features=2, n_classes=2, n_samples=300)

# 특징과 종속 변수 각각을 학습 데이터와 검증 데이터로 나누기
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 서포트 벡터 머신 모델 생성
model = SVC(gamma='auto')

model.fit(X_train, y_train)    # 학습
y_pred = model.predict(X_test) # 예측
accuracy_score(y_pred, y_test) # 평가

Footnotes

1. a real-valued function that quantifies the similarity between two objects

2. 커널svm 참고